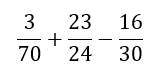Primero necesitamos hablar sobre las fracciones.
Una fracción es una división entre un número que va a ser dividido (dividendo) al que llamamos numerador, y el número que divide (divisor) que llamamos denominador.
Entonces, ¿Cómo hacer una suma entre fracciones? Debes tener el mismo denominador si quieres sumar los numeradores. Para este propósito debemos saber como hacer el mínimo común múltiplo.
El mínimo común múltiplo es calculado cuando tenemos varios números. Debemos calcular los números primos que obtienen ese número cuando tu los multiplicas.
Un número primo es un número que sólo puede ser dividido exactamente por 1 y por si mismo. Por ejemplo 7 solo puede ser dividido por 1 y 7 así que es un número primo. Por otro lado 14 puede ser dividido por 1,2,7 y 14 así que no es primo.
Un número primo es un número que sólo puede ser dividido exactamente por 1 y por si mismo. Por ejemplo 7 solo puede ser dividido por 1 y 7 así que es un número primo. Por otro lado 14 puede ser dividido por 1,2,7 y 14 así que no es primo.
Por ejemplo los números 70, 24,30:
70 es par, así que es divisible entre 2 y obtenemos 35. 35 termina en 5 así que es divisible entre 5 y obtenemos 7 que es un número primo así que es el último número que necesitamos obtener. Podemos expresarlo de la siguiente manera:
Ahora que hemos descompuesto los números en sus números primos podemos calcular el mínimo común múltiplo tomando los diferentes números obtenidos con su máximo exponente y los multiplicas:
Ahora vamos a usar estos números para hacer las fracciones:
Tenemos los mínimos común múltiplos de los denominadores, la solución se obtiene multiplicando el numerador y el denominador por el mismo número hasta que obtengamos el mínimo común múltiplo en el denominador.
Y ahora podemos sumarlos o restarlos:
Esta es la base del cálculo fraccional para sumas y diferencias. Espero que te haya servido. ¡Un saludo y nos vemos en la próxima ocasión!