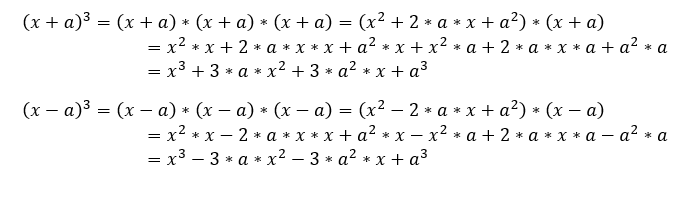Un polinomio es una combinación de variables. Las variables deben cumplir la igualdad para ser llamada ecuaciones. Cuando estamos en 2D solo necesitamos una ecuación para obtener una curva.
Un ejemplo de curva dado por un polinomio sería:
Habitualmente la variable “x” es llamada variable independiente, y la “y” es llamada variable dependiente porque damos valores arbitrarios a la "x" y obtenemos valores para "y". La variable “y” se escribe “y(x)” ó f(x).
Las operaciones suma y diferencia con polinomios deben ser hechas con variables elevadas al mismo exponente. Tu puedes sumar los constantes coeficientes de esas variables.
Las operaciones suma y diferencia con polinomios deben ser hechas con variables elevadas al mismo exponente. Tu puedes sumar los constantes coeficientes de esas variables.
El grado del polinomio sería el valor máximo entre los exponentes.
El grado muestra la cantidad de ceros del problema. Un cero aparece cuando y=0, esto ocurre cuando la curva corta el eje de las "x". Así que en el ejemplo gráfico anterior podemos encontrar tres ceros: uno entre -8 y -6, otro entre -2 y 0 y el último entre 2 y 4.
Para encontrar los ceros de los polinomios existen soluciones analíticas (una fórmula para resolver el problema de forma exacta) hasta grado 5. Para grados mayores la solución analítica no existe.
El problema típico es resolver el problema de grado 2:
Que tiene dos posibles soluciones de "x":
Finalmente mostraré como realizar el producto de un binomio. Un binomio es un polinomio de dos términos . Los polinomios se pueden multiplicar entre ellos para obtener nuevos polinomios. El producto de un binomio es el producto más fácil entre polinomios. Los principales productos:
En particular:
Y si multiplicamos una vez más: